
BPNN - Предсказатель на основе самообучающейся нейронной сети
Предсказатель на основе самообучающейся нейронной сети.
Предлагается индикатор использующий нейронную сеть прямого распространения (feedforward neural network), которая самообучается методом Обратного Распространения Ошибки (backpropagation). Сеть загружается через DLL файл, исходный C++ код которого прилагается.
Нейронная сеть это ничто иное как нелинейная модель выходов как функция входов. На входы подаются данные задаваемые пользователем, например выборки временного ряда. Смысл выходных данных также задаётся пользователем, например сигналы 1=buy/0=sell. Структура сети опять же задаётся пользователем. Сеть прямого распространения состоит из
-входного слоя (input layer), элементами которого являются входные данные,
- скрытых слоёв (hidden layers), состоящих из вычислительных узлов называемых нейронами (neurons) и
- выходного слоя (output layer), который состоит из одного или нескольких нейронов, выходы которых являются выходами всей сети.
Все узлы соседних слоёв связаны между собой. Эти связи называются синапсами (synapses). Каждый синапс имеет вес (weight w[i,j,k]), на которой умножаются данные передаваемые по синапсу. Данные передвигается слева направа т.е. от входов сети к её выходам. Отсюда и название, "сеть прямого распространения". Общий пример этой сети изображён на рисунке внизу
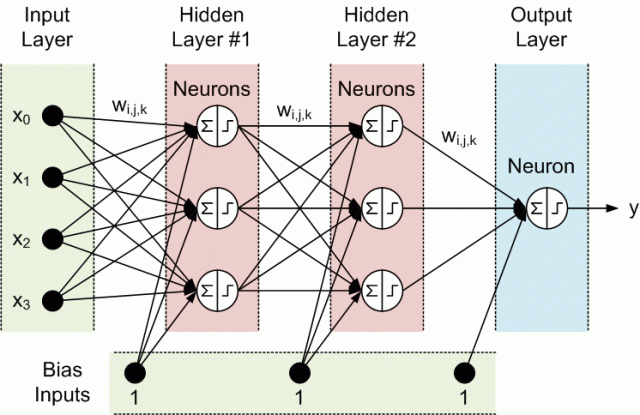
Данные перерабатываются нейронами за два шага:
1. Все входы, помноженные на соответствующие веса, сначала суммируются
2. Затем получившиеся суммы обрабатываются функцией активации нейрона (activation or firing function) и посылаются на единственный выход.
Смысл функции активации нейрона заключается в моделировании работы нейрона мозга: нейрон срабатывает только после того как информация достигла определённого порога. В математическом аспекте, эта функция как раз и придаёт нелинейность сети. Без неё, нейронная сеть была бы линейной авторегрессионной моделью (linear prediction model). В прилагаемых библиотечных функциях возможен выбор трёх функций активации нейрона
* сигмоидальная функция sigm(x)=1/(1+exp(-x)) (#0)
* гиперболический тангенс tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
* рациональная функция x/(1+|x|) (#2)
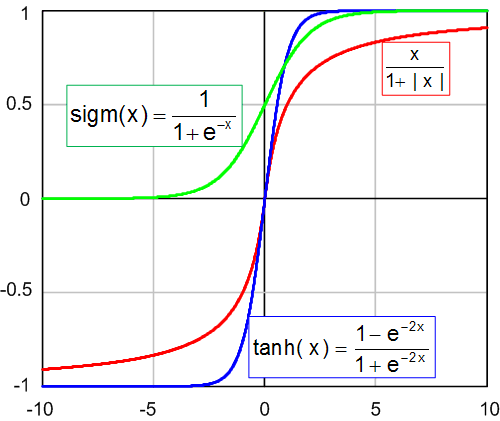
Порог активации этих функций равен 0. Этот порог может быть сдвинут по горизонтальной оси за счёт дополнительного входа нейрона называемом входом смещения (bias input), которому приписан определённый вес таким же образом как и к другим входам нейрона.
Таким образом, количество входов, слоев, нейронов в каждом слою и веса входов нейронов полностью определяют нейронную сеть, т.е. нелинейную модель, которую она создаёт. Чтобы пользоваться этой моделью необходимо знать веса. Веса вычисляются путём обучения сети на прошлых данных: на входы сети подаются нескольков наборов входных и соответствующих выходных данных и рассчитывается среднеквадратичная ошибка отклонения выхода сети от тестируемого. Цель обучения сети заключается в уменьшении этой ошибки путём оптимизации весов. Существуют несколько методов оптимизации, среди которых основными эвляются метод Обратного Распространения Ошибки (ОРО) и метод генетической оптимизации.
Прилагаемые файлы:
* BPNN.dll - библиотечный файл
* BPNN.zip - архив всех файлов необходимых для создания ДЛЛ файла
* BPNN Predictor.mq4 - индикатор предсказывающий будущее значение цены
* BPNN Predictor with Smoothing.mq4 - индикатор предсказывающий будущее значение цены, сглаженной ЕМА
Библиотечный файл BPNN.cpp содержит две функции: Train() и Test(). Train() предназначен для обучения сети для предоставленных входных и выходных данных. Test() предназначен для вычисления выходных данных на основе весов полученных после прогона Train().
Входными (зелёный цвет) и выходными (синий цвет) параметрами функции Train() являются:
double inpTrain[] - обучивающие входные данные (старый первый)
double outTarget[] - обучивающие выходные данные (старый первый)
double outTrain[] - выходы сети после обучения
int ntr - количество обучающих наборов входы-выходы
int UEW - ключ управляющий использованием внешних значений для инициализации весов (1=используем extInitWt[], 0=используем случайные числа)
double extInitWt[] - исходные значения весов
double trainedWt[] - значения весов после обучения
int numLayers - количество слоев в сети включая входной, скрытые и выходной
int lSz[] - одомерный массив размера numLayers, в котором хранятся количества нейронов в каждом слою. lSz[0] задаёт количество входов сети
int AFT - тип функции активации (0-сигмоидальная, 1-гиперболический тангенс, 2-рациональная)
int OAF - ключ использования функции активации в выходны нейронах (1=используем функцию активации, 0=нет)
int nep - максимальное количество обучающих шагов (эпох). Эпоха состоит из проверки всех обучающих наборов.
double maxMSE - среднеквадратичная ошибка, при которой обучения останавливается.
Входными (зелёный цвет) и выходными (синий цвет) параметрами функции Test() являются:
double inpTest[] - входные данные (старый первый)
double outTest[] - выходные данные
int ntt - колчиство наборов в входных и выходных данных
double extInitWt[] - исходные значения весов
int numLayers - количество слоев в сети включая входной, скрытые и выходной
int lSz[] - одомерный массив размера numLayers, в котором хранятся количества нейронов в каждом слою. lSz[0] задаёт количество входов сети
int AFT - тип функции активации (0-сигмоидальная, 1-гиперболический тангенс, 2-рациональная)
int OAF - ключ использования функции активации в выходны нейронах (1=используем функцию активации, 0=нет)
Использование функции активации в выходных нейронах зависит от характера выходны данных. Если выходами сети являются биноминальные сигналы (0/1 или -1/1), то нужно использовать функцию активации (OAF=1). Причём учтите что для функции №0, уровни сигнала 0 и 1, а для функций №1 и 2 уровни -1 и 1. Если выходом сети является предсказание цены, то функция активации в выходном слое не нужна (OAF=0).
Примеры индикаторов использующих нейронную сеть:
BPNN Predictor.mq4 - предсказывает будущие цены. Входными параметрами сети являются относительные приращения цен:
x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0
где delay[i] берётся из ряда Фибоначи. Выходом сети является предсказываемое относительное приращение будущей цены. Фунцкия активации в выходном слое отключена.
Входными параметрами индикатора являются
extern int lastBar - номер последнего бара
extern int futBars - количество будущих предсказываемых баров
extern int numLayers - количество слоев в сети включая входной, скрытые и выходной
extern int numInputs - количество входов сети
extern int numNeurons1 - количество нейронов в слое №1
extern int numNeurons2 - количество нейронов в слое №2
extern int numNeurons3
extern int numNeurons4
extern int numNeurons5
extern int ntr - количество обучающих наборов входы-выходы
extern int nep - максимальное количество обучающих шагов (эпох)
extern int maxMSEpwr - экспонента используемая для расчёта максимальной допустимой среднеквадратической ошибки обучения maxMSE=10^maxMSEpwr
extern int AFT - тип функции активации (0-сигмоидальная, 1-гиперболический тангенс, 2-рациональная)
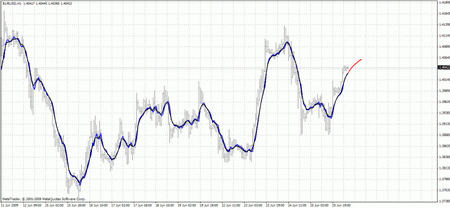
Индикатор выдаёт такую картинку, где
* красный цвет - предсказания от последней цены Open
* чёрный цвет - прошлые тренировочные цены Open, по котором (как ожидаемым выходным данным) проводилось обучение сети
* синий цвет - выходы обученной сети на тренировочных данных

BPNN Predictor with Smoothing.mq4 - тоже предсказывает цены, но с предварительным сглаживанием цен экспоненциальной скользящей средней (EMA) с периодом smoothPer.
Установка файлов:
1. Копируйте приложенный BPNN.DLL файл в C:\Program Files\MetaTrader 4\experts\libraries
2. Включайте использование DLL в метатрейдере: Tools - Options - Expert Advisors - Allow DLL imports
Если приложенный DLL файл не работает, то компилируйте сами. Все необходимые файлы содержатся в BPNN.zip.
Советы:
* Сеть с 3-ми слоями (numLayers=3: один входной, один скрытый и один выходной) достаточна для подавляющего большинства применений. По теоремe Cybenko (1989) сеть с одним скрытым слоем может моделировать любую непрерывную нелинейную фунцкию и сеть с двумя скрытыми слоями способна описать функцию с разрывами (http://en.wikipedia.org/wiki/Cybenko_theorem):

* Количество нейронов в скрытом слую определяйте экспериментально. В литературе встречаются такие рекомендации: кол-во скрытых нейронов = (кол-во входов + кол-во выходов)/2, либо SQRT(кол-во входов * кол-во выходов). Следите за сообщениями о среднеквадратичной ошибки обучения в окне experts метатрейдера.
* Для получения хорошего обобщения, количество обучающих выборок должно в 2-3 раза превышать количество оптимизируемых весов. Например, в опубликованных примерах, количество весов равно (12+1)*5 на входах скрытого слоя плюс (5+1) на входах выходоного слоя, т.е. 71. Поэтому количество обучающих выборок должно быть по крайней мере 142. Концепт обобщения объяснён на рисунке внизу для одномерного случая y(x).
* Увеличения количества обучающих эпох может не повысить точность предсказаний на тестируемых данных даже если ошибка обучения (MSE) уменьшилась. При большом количестве весов сеть становится переученной (см объяснения внизу).
* Входные данные должны преобразоваться в стационарный ряд. Цены сами по себе таковым рядом не являются. Рекомендуется также нормализовывать входные данные к диапазону -1..1.
На этом графике показана линейная функция y=b*x (x-вход, y-выход) с добавленным шумом к выходам. Из-за этого шума, измерения функции (чёрные точки) не лежат на прямой. Функция y=f(x) может быть смоделирована нейронной сетью. Сеть с большим количеством весов (степеней свободы) способна уменьшить ошибку обучения по всем имеюшимся измерениям до нуля и описать тренировочные выходные данные плавной кривой. Но эта кривая (показана красным цветом) не имеет ничего общего с нашей линейной фунцкией y=b*x (показана зелёным цветом). Использование такой сети для предсказания будущих значений функции y при новых входных значениях x приведёт к большим ошибкам так как шум не предсказуем.

| Прикрепленный файл | Размер |
|---|---|
| BPNN.zip | 58.75 кб |


Советник может и хорош, может
Советник может и хорош, может и работал\ет но у меня упорно не хочет ставиться на график)) разрешил импорт dll в настройка, ипмортировал dll в билиотеку МТ4 и все равно не работает. сейчас перекомпирую во всех возожных С но что то сомневаюсь что он встанет как надо. Одпишитесь кто с этим совеником работал и стоит ли игра свечь.
Подскажите как правильно
Подскажите как правильно загрузить индикатор. Он у меня показывает прогноз в виде горизонтальной красной черты, и всё мертвый. Какие настройки менять или оставлять по умолчанию?
Не хочет присоединяться к
Не хочет присоединяться к графику
Когда присоединяете индикатор
Когда присоединяете индикатор в свойствах/Общие нажмите галочку Разрешить Импорт DLL
Подскажите как правильно
Подскажите как правильно установить индикатор. Какие настройки менять? Заранее спасибо.